なぜ商品やサービスの持つ各属性の重要性を数値化して把握することが必要なのだろうか。それは商品やサービスの供給者側となって考えてみれば明らかです。あなたがパソコンの供給者側になったときを想像してください。最先端のスペックで洗練されたデザインを持ち長期間のアフターサービスで、ソフトが充実しており、なおかつ一般的な普及帯価格で顧客に提供できたら、かなりの市場シェアを取ることができるかもしれない。しかし、これは非常に困難であることは明白です。最先端のスペックと一般的な普及帯価格の両立は困難であるし、その他も同様です。つまり、供給者側として、どこに一番ニーズがあるか、言い換えればどこの市場が有望であるかを把握することが非常に重要です。
ここではR言語のconjointパッケージを用いて実際のコンジョイント分析について説明します。データはconjointパッケージに付属するサンプルデータteaを用いました。
Conjointパッケージのインストールと読み込み
まず、R言語でコンジョイント分析を行うための準備を行います。Rを立ち上げ次のコマンドを実行します。
# conjointパッケージのインストール
install.packages("conjoint")
# conjointパッケージの読み込み
library("conjoint")
# teaデータの読み込み
data(tea)
商品を属性・水準に分解する
あなたがお茶専門店の経営者で品揃えに悩んでいたとし、どのような商品が顧客に支持されるか顧客アンケートをとり、評価点を10点満点で採点してもらうことにしたとします。そこで、お茶を以下の属性および水準に分解したとします。
- price:low、medium、highの3水準
- variety:black、green、redの3水準
- kind:bags、granulated、leafyの3水準
- aroma:yes、noの2水準
具体的には、price、variety、king、aromaがそれぞれlow、black、bags、yesの商品の評価点は何点か。price、variety、king、aromaがそれぞれmedium、green、granulated、noの商品の評価点は何点かという具合です。つまり、アンケート項目としては3×3×3×2=54項目となるが、アンケートの質問数としては多いと感じるのでしょう。そこで、直交表というものを用います。これを用いれば、質問数を減らして、なおかつ評価されていない残りの商品も評価できます。
補足として、なぜこのように質問するのか答えます。例えば、priceからlow、medium、highを一つ選んで、varietyからblack、green、redを一つ選んで・・・といった方法の場合は、おそらく質問が「あなたが今すぐ飲みたいお茶はどのようなものですか」といったものになりアンケート回答者から得られるデータが一つとなってしまいます。果たしてそれは正しいデータでしょうか。アンケートを取った時点では正しいものかもしれないが、一週間後同じ人に同様のアンケートを取った場合、同じ結果が得られるでしょうか。おそらく違うものになっていると思います。つまり、このようなデータを集めても活用するときにはあまり意味のないものになっている可能性があります。それよりもどの項目を重要視するか、つまり購買行動を知るほうがより有意義に活用できます。
直交表を作成する
直交表を作成する場合は、自力で作成することは大変煩雑なためプログラムの力を使う必要があります。R言語で直交表を作る手順は以下のようになります。
# 因子の組み合わせを作成
experiment<-expand.grid(
(con) price=c("low","medium","high"),
(con) variety=c("black","green","red"),
(con) kind=c("bags","granulated","leafy"),
(con) aroma=c("yes","no"))
# 因子の直交表を作成
design<-caFactorialDesign(data=experiment,type="orthogonal")
# 因子の直交表を表示
print(design)
(out) price variety kind aroma
(out)7 low red bags yes
(out)11 medium black granulated yes
(out)24 high green leafy yes
(out)30 high black bags no
(out)32 medium green bags no
(out)40 low green granulated no
(out)45 high red granulated no
(out)46 low black leafy no
(out)53 medium red leafy no
# 因子の直交表をコード化
code<-caEncodedDesign(design)
# コード化された直交表の表示
print(code)
(out) price variety kind aroma
(out)7 1 3 1 1
(out)11 2 1 2 1
(out)24 3 2 3 1
(out)30 3 1 1 2
(out)32 2 2 1 2
(out)40 1 2 2 2
(out)45 3 3 2 2
(out)46 1 1 3 2
(out)53 2 3 3 2
# 相関係数の表示
print(cor(code))
(out) price variety kind aroma
(out)price 1 0 0 0
(out)variety 0 1 0 0
(out)kind 0 0 1 0
(out)aroma 0 0 0 1
因子の直交表で表示されている(low,red,bags,yes)、・・・(medium,red,lefy,no)までの9通りの商品をアンケートに載せれば良いです。全体の54通りからみればずいぶんと減りました。なぜこのようなことができるのかというと、最後の相関係数の表示を見ると、異なる要素間での相関係数が0となっているためです。つまり、9通りの商品から4つの要素がそれぞれ独立して取り出せることを意味しています。
ここではサンプルデータteaの中にすでにあるものを用います。
# 商品プロファイル-アンケートに記載する13個の商品
print(tprof)
(out) price variety kind aroma
(out)1 3 1 1 1
(out)2 1 2 1 1
(out)3 2 2 2 1
(out)4 2 1 3 1
(out)5 3 3 3 1
(out)6 2 1 1 2
(out)7 3 2 1 2
(out)8 2 3 1 2
(out)9 3 1 2 2
(out)10 1 3 2 2
(out)11 1 1 3 2
(out)12 2 2 3 2
(out)13 3 2 3 2
# 各水準のラベル
print(tlevn)
(out) levels
(out)1 low
(out)2 medium
(out)3 high
(out)4 black
(out)5 green
(out)6 red
(out)7 bags
(out)8 granulated
(out)9 leafy
(out)10 yes
(out)11 no
アンケート分析
100人にアンケートを行い13個の商品をそれぞれ10点満点で評価してもらったとします。その結果が以下のようになったとします。各行はアンケート回答者一人ひとりの回答であり、各列は商品に該当します。
# 最初のデータのみ表示
head(tprefm)
profil1 profil2 profil3 profil4 profil5 profil6 profil7 profil8 profil9 profil10 profil11 profil12 profil13
1 8 1 1 3 9 2 7 2 2 2 2 3 4
2 0 10 3 5 1 4 8 6 2 9 7 5 2
3 4 10 3 5 4 1 2 0 0 1 8 9 7
4 6 7 4 9 6 3 7 4 8 5 2 10 9
5 5 1 7 8 6 10 7 10 6 6 6 10 7
6 10 1 1 5 1 0 0 0 0 0 0 1 1
これをもとにR言語でコンジョイント分析を行うと以下のようになります。ここでは、Conjoint関数を実行した際に出力されるデータの読み方については省略させていただき、同時に出力されるグラフを元に説明していきます。
Conjoint(tprefm, tprof, tlevn)
Call:
lm(formula = frml)
Residuals:
Min 1Q Median 3Q Max
-5,1888 -2,3761 -0,7512 2,2128 7,5134
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3,55336 0,09068 39,184 < 2e-16 ***
factor(x$price)1 0,24023 0,13245 1,814 0,070 .
factor(x$price)2 -0,14311 0,11485 -1,246 0,213
factor(x$variety)1 0,61489 0,11485 5,354 1,02e-07 ***
factor(x$variety)2 0,03489 0,11485 0,304 0,761
factor(x$kind)1 0,13689 0,11485 1,192 0,234
factor(x$kind)2 -0,88977 0,13245 -6,718 2,76e-11 ***
factor(x$aroma)1 0,41078 0,08492 4,837 1,48e-06 ***
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1
Residual standard error: 2,967 on 1292 degrees of freedom
Multiple R-squared: 0.09003, Adjusted R-squared: 0.0851
F-statistic: 18.26 on 7 and 1292 DF, p-value: < 2,2e-16
[1] "Part worths (utilities) of levels (model parameters for whole sample):"
levnms utls
1 intercept 3,5534
2 low 0,2402
3 medium -0,1431
4 high -0,0971
5 black 0,6149
6 green 0,0349
7 red -0,6498
8 bags 0,1369
9 granulated -0,8898
10 leafy 0,7529
11 yes 0,4108
12 no -0,4108
[1] "Average importance of factors (attributes):"
[1] 24,76 32,22 27,15 15,88
[1] Sum of average importance: 100,01
[1] "Chart of average factors importance"
以下の「price-utility」のグラフからpriceに対してlowの商品が最も高評価となっており、反対にpriceに対してmediumの商品が最も低評価となっていることが分かります。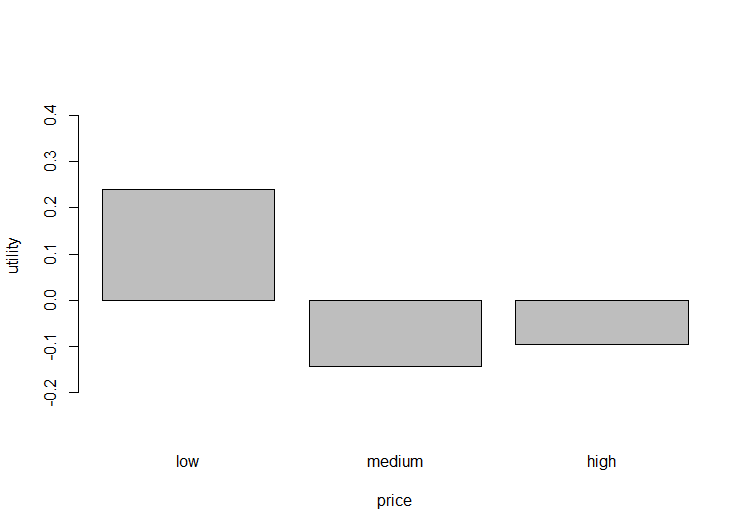
以下の「variety-utility」のグラフからvarietyに対してblackの商品が最も高評価となっており、反対にvarietyに対してredの商品が最も低評価となっていることが分かります。
以下の「kind-utility」のグラフからkingに対してleadyの商品が最も高評価となっており、反対にgranulatedの商品が最も低評価となっていることが分かります。
以下の「aroma-utility」のグラフからaromaがyesの商品は高評価で、noの商品は低評価となっていることが分かります。
以下の「Factors-Average importance」のグラフからvariety、kind、price、aromaの順で全体的な評価に影響を与えることが分かります。
以上をまとめると、priceがlow、varietyがblackまたはgreen、kindがbagsまたはleafy、aromaがyesの商品が評価が比較的評価が高い商品であることが分かります。また、priceが全体的に与える影響が低いことと、priceのhighが比較的影響が少ないことから、priceがhighの商品も魅力あるものとしてみることができます。
クラスター分析
R言語のconjointパッケージを用いると簡単にクラスター分析ができるので簡単に見ておきます。クラスター分析を行えば、アンケート回答が似通った回答者で分類することができます。以下は5つで分類したものです。Clustering vectorをみると回答者順にどのクラスターに属するのかが分かります。
# 5つのクラスターに分類
caSegmentation(tprefm,tprof,5)
K-means clustering with 5 clusters of sizes 23, 12, 8, 37, 20
Cluster means:
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
1 3.493217 4.425000 3.103261 3.632348 5.346739 1.476000 4.380348 2.1383043 1.338304 1.0801739 2.799174 4.5194783 5.5716522
2 3.098333 6.501167 3.834500 3.098333 2.717833 5.776750 4.160083 7.1300000 2.930000 7.5690000 5.596667 4.1600833 2.4267500
3 5.442000 4.105000 7.030000 7.042000 6.005000 6.646500 6.996500 5.9345000 6.909500 4.1855000 5.584500 8.5965000 8.2715000
4 5.464919 2.646784 1.257595 4.659514 1.781919 3.988622 1.177811 0.9651081 3.029973 0.1449459 3.613757 0.3724054 0.5183514
5 4.930900 6.352900 3.822900 8.470900 6.372900 3.554900 3.574900 1.5366000 2.186600 1.4904500 8.256600 7.1149000 7.0349000
Clustering vector:
[1] 1 2 5 3 3 4 1 2 5 5 5 5 4 4 4 4 2 4 1 4 1 5 4 1 1 1 2 1 3 3 4 1 2 5 5 5 5 4 4 4 4 2 4 1 4 1 5 4 4 4 1 4 4 4 5 5 4 3 1
[60] 1 4 4 1 1 2 1 4 4 4 5 5 4 1 2 5 3 3 4 1 1 2 1 3 5 4 4 4 4 2 4 2 4 1 4 1 5 4 2 5 5
Within cluster sum of squares by cluster:
[1] 1243.8157 396.4692 278.5669 1399.7583 721.3690
(between_SS / total_SS = 56.4 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size"
まとめ
ここまで、コンジョイント分析について一通りみてきました。コンジョイント分析を行えば、商品やサービスの持つ各属性がどの程度影響を与えているのかが数値としてはっきりと示されることが分かったと思います。つまり、より具体的に顧客に対して訴求すべきポイントがどこあるのかを知ることができます。今まで、経験や勘で商品やサービスの設計・提供を行っていたら、一度コンジョイント分析を活用して商品やサービスの設計を行ってみてはどうでしょうか。

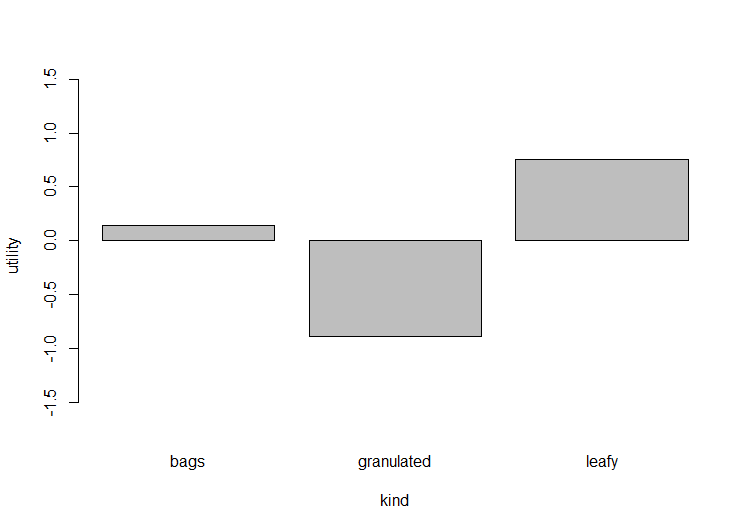
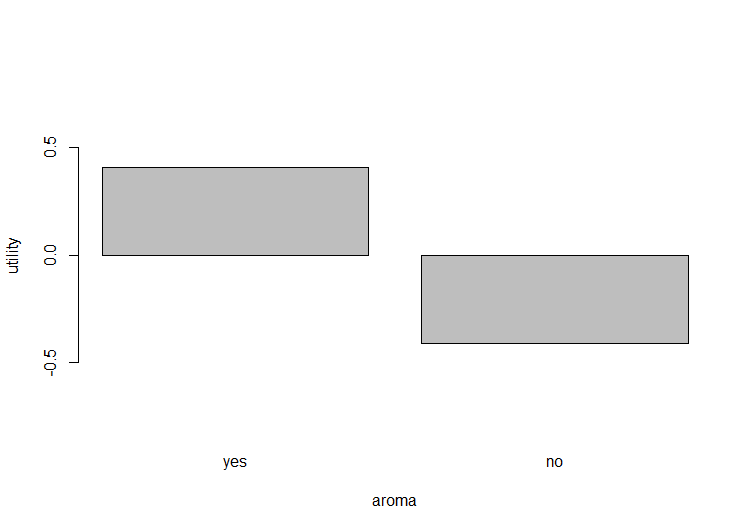
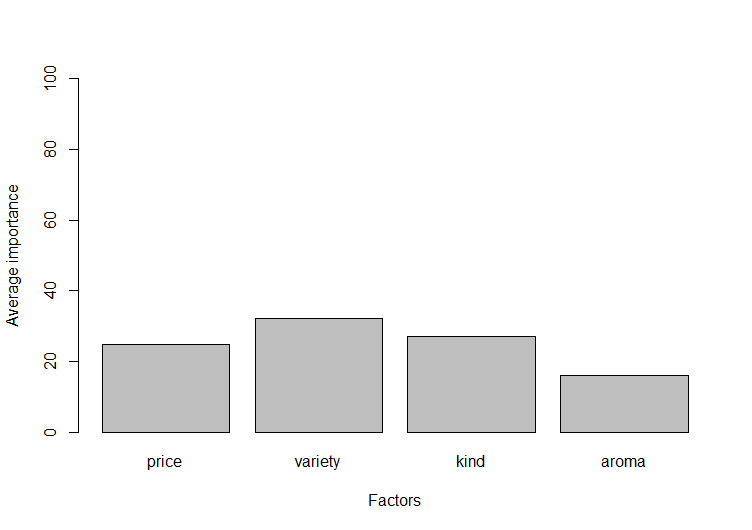



ピンバック:conjoint分析の資料 | 科学の箱