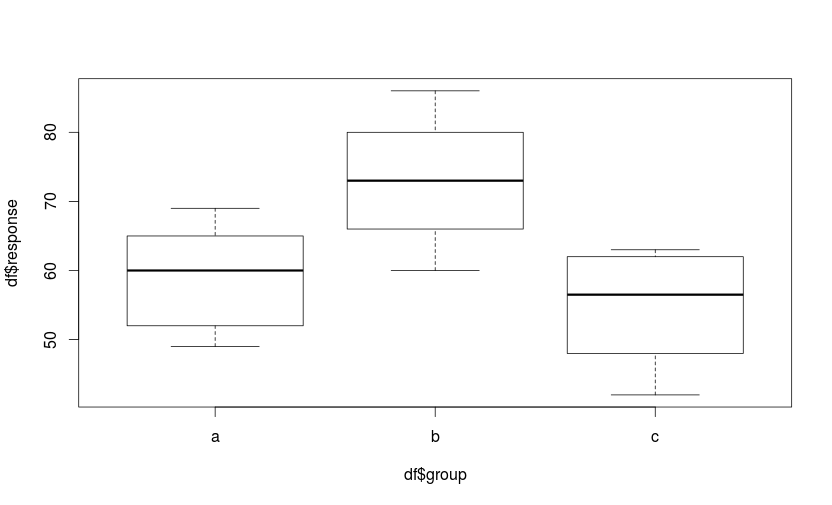
スティール(Steel)法とは、ダネット(Dunnett)法の多重比較に対応するノンパラメトリックな多重比較です。
スティール法を簡単に言うと、正規分布を仮定しない1つの対照群と2つ以上の処理群間を順位を用いて多重比較で調べる方法です。
スティール法を簡単に言うと、正規分布を仮定しない1つの対照群と2つ以上の処理群間を順位を用いて多重比較で調べる方法です。
Rで、スティール法を使う場合は、「スティール(Steel)の方法による多重比較」のページにソースコードが紹介されています。
ここでは、このソースコードを少しばかり改変したものをご紹介します。主な対応は次のとおりです。
- 引数をformula形式に対応(response ~ group)
- 引数で対照群を指定
- 返り値にP値を追加
- 返り値をデータフレームに変更
- 片側検定に対応
P値は、RのパッケージRcmdrPlugin.EZRのソースコードを参考にさせていただきました。
P値の計算で、mvtnormパッケージを用いているので、あらかじめインストールおよび有効化しておきます。
install.packages('mvtnorm')
library(mvtnorm)
次が改変したソースコードです。標準パッケージstats内のソースコードも参考にさせていただきました。
steel.test <- function(x, ...) UseMethod("steel.test")
steel.test.default <-
function(x, g, control = NULL, alternative = c("two.sided", "less", "greater"), ...)
{
alternative <- match.arg(alternative)
if (is.list(x)) {
if (length(x) < 2L)
stop("'x' must be a list with at least 2 elements")
if (!missing(g))
warning("'x' is a list, so ignoring argument 'g'")
DNAME <- deparse(substitute(x))
x <- lapply(x, function(u) u <- u[complete.cases(u)])
if (!all(sapply(x, is.numeric)))
warning("some elements of 'x' are not numeric and will be coerced to numeric")
k <- length(x)
l <- sapply(x, "length")
if (any(l == 0L))
stop("all groups must contain data")
g <- factor(rep.int(seq_len(k), l))
x <- unlist(x)
}
else {
if (length(x) != length(g))
stop("'x' and 'g' must have the same length")
DNAME <- paste(deparse(substitute(x)), "and",
deparse(substitute(g)))
OK <- complete.cases(x, g)
x <- x[OK]
g <- g[OK]
if (!all(is.finite(g)))
stop("all group levels must be finite")
g <- factor(g)
k <- nlevels(g)
if (k < 2L)
stop("all observations are in the same group")
}
if (is.null(control)) {
control <- levels(g)[1]
}
if (!any(levels(g) == control)) {
stop("The dataset doesn't contain this control group!")
}
# calculate ρ
get.rho <- function(ni)
{
l <- length(ni)
rho <- outer(ni, ni, function(x, y) { sqrt(x/(x+ni[1])*y/(y+ni[1])) })
diag(rho) <- 0
return(sum(rho[-1, -1]) / (l - 2) / (l - 1))
}
## number of data in each group
ni <- table(g)
## number of group
a <- length(ni)
## data of control group
xc <- x[g == control]
## number of data in control group
n1 <- length(xc)
## decide ρ
rho <- ifelse(sum(n1 == ni) == a, 0.5, get.rho(ni))
vc <- c()
vt <- c()
vp <- c()
for (i in levels(g)) {
if(control == i) {
next
}
## ranking group i,j
r <- rank(c(xc, x[g == i]))
## test statistic
R <- sum(r[1 : n1])
## total number of the 2 group data
N <- n1 + ni[i]
## expectation of test statistic
E <- n1 * (N + 1) / 2
## variance of test statistic
V <- n1 * ni[i] / N / (N - 1) * (sum(r^2) - N * (N + 1)^2 / 4)
## t.value
t <- (R - E) / sqrt(V)
# calculate p.value
corr <- diag(a - 1)
corr[lower.tri(corr)] <- rho
pmvt.lower <- -Inf
pmvt.upper <- Inf
if (alternative == "less") {
pmvt.lower <- -t
pmvt.upper <- Inf
}
else if (alternative == "greater") {
pmvt.lower <- t
pmvt.upper <- Inf
}
else {
t <- abs(t)
pmvt.lower <- -t
pmvt.upper <- t
}
p <- 1 - mvtnorm::pmvt(lower = pmvt.lower, upper = pmvt.upper, delta = numeric(a - 1), df = 0, corr = corr, abseps = 0.0001)
vc <- c(vc, paste(i, control, sep = ':'))
vt <- c(vt, t)
vp <- c(vp, p)
}
df <- data.frame(comparison = vc,
t.value = vt,
rho = rho,
p.value = vp)
rownames(df) <- NULL
return(df)
}
steel.test.formula <-
function(formula, data, subset, na.action, ...)
{
if(missing(formula) || (length(formula) != 3L))
stop("'formula' missing or incorrect")
m <- match.call(expand.dots = FALSE)
if(is.matrix(eval(m$data, parent.frame())))
m$data <- as.data.frame(data)
## need stats:: for non-standard evaluation
m[[1L]] <- quote(stats::model.frame)
m$... <- NULL
mf <- eval(m, parent.frame())
if (!is.factor(mf[[2]])) {
mf[[2]] <- factor(mf[[2]])
}
if(length(mf) > 2L) {
stop("'formula' should be of the form response ~ group")
}
names(mf) <- NULL
y <- do.call("steel.test", append(as.list(mf), list(...)))
y
}
両側検定
元のソースコードと結果が一致するかを確認します。次が元のソースコードの結果で、そのまま引用させて頂いきました。
data <- c(
50, 55, 65, 63, 60, 68, 69, 60, 52, 49, # 第 1 群(対照群)のデータ,10 例
80, 86, 74, 66, 79, 81, 70, 62, 60, 72, # 第 2 群(処理群)のデータ,10 例
42, 48, 58, 63, 62, 55, 63, 60, 53, 45 # 第 3 群(処理群)のデータ,10 例
)
group <- rep(1:3, each=10) # 群を表す数値
Steel(data, group)
t rho
1:2 2.952566 0.5
1:3 1.175674 0.5
次が改変したソースコードの結果です。意図的に群を表すベクトルを文字列にして、formulaを用いています。
df <- data.frame(response = data, group = rep(letters[1:3], each = 10))
steel.test(response ~ group, data = df, control = "a")
comparison t.value rho p.value
1 b:a 2.952566 0.5 0.006100359
2 c:a 1.175674 0.5 0.392816990
結果が同様になることが確認できました。
片側検定
同様のデータで、片側検定を行った結果は次になります。
steel.test(response ~ group, data = df, control = "a", alternative = "less")
comparison t.value rho p.value
1 b:a -2.952566 0.5 0.9998987
2 c:a 1.175674 0.5 0.1978174
steel.test(response ~ group, data = df, control = "a", alternative = "greater")
comparison t.value rho p.value
1 b:a -2.952566 0.5 0.00305018
2 c:a 1.175674 0.5 0.95809243
追記
Rのバージョンが4.4.2では次のエラーが出て、動作しない事例をご報告いただきました。
上記のコードは以下のエラーが出ないように変更したコードになります。
エラーの原因は、eval()関数またはparent.frame()関数の挙動がバージョン間で異なっておりました。
ご報告いただいた方へ、この場を借りてお礼申し上げます。
steel.test.default(c(50, 55, 65, 63, 60, 68, 69, 60, 52, 49, でエラー:
all group levels must be finite
R多重検定 スティール(Steel)法